Казімірський Петро Степанович
доктор фізико-математичних наук, професор
(26.11.1925 р. – 14.02.1990 р.)
 Петро Степанович Казімірський – відомий вчений у галузі алгебри. Його основні наукові результати відносяться до теорії кілець, лінійної і диференціальної алгебри. Він започаткував і розвинув новий напрямок лінійної алгебри, що пов’язаний з розкладністю матричних многочленів на множники та створенням методів розв’язування матричних рівнянь. Значну увагу вчений приділяв дослідженню проблем лінійної алгебри в контексті загальної теорії асоціативних кілець.
Петро Степанович Казімірський – відомий вчений у галузі алгебри. Його основні наукові результати відносяться до теорії кілець, лінійної і диференціальної алгебри. Він започаткував і розвинув новий напрямок лінійної алгебри, що пов’язаний з розкладністю матричних многочленів на множники та створенням методів розв’язування матричних рівнянь. Значну увагу вчений приділяв дослідженню проблем лінійної алгебри в контексті загальної теорії асоціативних кілець.
П.С. Казімірський народився 26 листопада 1925 року у м. Бершадь Вінницької області. У 1940 році він разом із сім’єю переїхав до м. Львова. Тут у 1943 році закінчив гімназію. У період 1943–1944 років навчався у Львівському медичному інституті (нині — Львівський національний медичний університет імені Данила Галицького). У липні-грудні 1944 року брав участь у боях за визволення Польщі від німецьких загарбників. Після закінчення війни П.С. Казімірський поступив на фізико-математичний факультет Львівського університету імені Івана Франка, деканом якого у той час був знаменитий математик – Стефан Банах. Під час навчання на факультеті він слухав лекції таких відомих математиків, як Я.Б. Лопатинський, Л.І. Волковиський, О.С. Кованько, І.Т. Соколов, Г.М. Савін, М.О. Зарицький, В.Й. Левицький та інші. Його оточувало прекрасне студентське середовище – у цей час на факультеті навчались також згодом добре відомі вчені: Я.С. Підстригач, В.Я. Скоробогатько, С.Д. Берман, В.Е. Лянце та ін. Це спонукало студентів швидко визначатися з науковими інтересами та розпочинати власні дослідження. Відвідуючи науковий семінар Я.Б. Лопатинського, П.С. Казімірський серйозно зацікавився проблемами алгебри, які мали застосування в теорії диференціальних рівнянь. У 1950 році П.С. Казімірський закінчив університет і з 1951 до 1970 р. працював асистентом, а згодом доцентом кафедри вищої математики Львівського політехнічного інституту. Поряд із педагогічною роботою він віддавав багато часу науковій діяльності. Під керівництвом професора Я.Б. Лопатинського підготував кандидатську дисертацію на тему: “Деякі загальні питання лінійної алгебри”, яку успішно захистив у Львівському університеті імені Івана Франка в 1957 році. Офіційними опонентами на захисті були Л.А. Калужнін та С.Д. Берман. Пізніше він організував науковий семінар з алгебри, який сприяв підготовці та захисту кандидатських дисертацій кількох його учнів – викладачів ЛПІ. У 1970 році П.С. Казімірський за ініціативою Я.С. Підстригача, який тоді керував сектором механіки і математики Фізико-механічного інституту АН УРСР, перейшов на постійну роботу до цього науково-дослідного закладу, де організував і очолив відділ алгебри, в якому працював до останніх днів свого життя. Незабаром у відділ прийшли працювати молоді випускники Львівського університету та інших вузів Львівщини, які згодом стали кандидатами та докторами фізико-математичних наук. Тоді ж був започаткований Львівський міський алгебраїчний семінар, яким Петро Степанович плідно керував. У ці роки до Львова приїжджали та робили доповіді такі відомі алгебраїсти, як професор МДУ Л.А. Скорняков, професор ЛДУ З.І. Боревич, академік АН БРСР, професор Д.А. Супруненко, керівник відділу алгебри ІМ СВ АН СРСР, професор Л.А. Бокуть, академік АН МРСР, професор В.А. Андрунакієвич, професори М.М. Постніков, А.А. Суслін, Ю.М. Рябухін, П.М. Гудивок, А.А. Бовді та багато інших науковців. Досягнення алгебраїчної школи П.С. Казімірського здобули широке визнання серед наукової громадськості країни. Підтвердженням цього стали проведення у Львові в 1987 році Всесоюзної алгебраїчної конференції за участю близько 500 алгебраїстів та Всесоюзного симпозіуму з теорії кілець, алгебр і модулів у 1990 році.
У Петра Степановича було багато захоплень (як він казав “гобі”): художня література, театр, музика, живопис. Він був добре обізнаний з творчістю львівських художників, з більшістю яких був особисто знайомий. З відомим митцем Володимиром Патиком його поєднувала багаторічна дружба. Щирі стосунки поєднували родину Казімірських з найближчим сусідом – знаменитим композитором Володимиром Івасюком. Петро Степанович часто сам виконував твори відомих композиторів на скрипці чи фортепіано. Добре грав у шахи. У затишній квартирі Петра Степановича та його дружини Стефанії Іванівни завжди були раді гостям. Відомі математики З.І. Боревич, Ю.А. Дрозд, О.І. Кострикін, Л.А. Скорняков, Д.К. Фаддеєв часто бували в них та хвалили неперевершену кулінарну майстерність господині.
Незважаючи на велику завантаженість науковою та організаційною роботою, П.С. Казімірський завжди знаходив час для спілкування зі студентами та аспірантами. Упродовж багатьох років він працював за сумісництвом професором кафедри алгебри і топології Львівського університету імені Івана Франка, читав основні курси та спецкурси, керував курсовими та дипломними роботами студентів. І все ж головним напрямом його діяльності була наукова робота в галузі алгебри. Наукові інтереси П.С. Казімірського відносяться до різних розділів лінійної алгебри та теорії кілець. Перша його наукова праця була присвячена узагальненню класичної теореми Кронекера – Капеллі про сумісність неоднорідних систем лінійних рівнянь на випадок систем з коефіцієнтами з довільної області головних ідеалів. У ній встановлено, що необхідними й достатніми умовами сумісності таких систем є рівність рангів прямої та розширеної матриць та подібність відповідних їх елементарних дільників. До того часу не було критерію сумісності лінійних неоднорідних рівнянь над некомутативними кільцями, які не є тілами. Для кілець усіх цілих алгебраїчних чисел такий критерій установив Штейніц, а для комутативних кілець головних ідеалів він був уже давно відомий. На основі отриманих результатів Петро Степанович сформулював критерії розв’язності лівосторонніх і правосторонніх лінійних матричних рівнянь першого степеня, матриці коефіцієнти яких мають елементи з фіксованої області головних ідеалів. Розв’язання цієї задачі сприяло виникненню ідеї про подання матриць над кільцями, зокрема над тілами, у вигляді добутку простих (у певному розумінні) множників. Проте навіть для класичного кільця многочленів від однієї змінної з коефіцієнтами з поля комплексних чисел такі питання виявились надзвичайно складними. Тому подальші дослідження в цьому напрямку він здійснював у термінах матричних многочленів. Методи, застосовані П.С. Казімірським під час вивчення задач лінійної алгебри над кільцями, ґрунтувалися на підходах, розроблених у межах класичної теорії некомутативних областей головних ідеалів. У зв’язку з цим природно постала задача про доповнення унімодулярних рядків до оборотних матриць, оскільки така процедура широко застосовувалася в цій теорії. Зауважимо, що зазначена задача тісно пов’язана з класифікацією кілець за стабільним рангом, яка виникла в контексті алгебраїчної K-теорії. Розв’язання проблем доповнюваності прямокутних матриць з унімодулярними рядками до оборотних та використання отриманих результатів у теорії кілець елементарних дільників він здійснював разом зі своїм учнем Ф.П. Луником. До цього ж напряму належать і роботи, виконані спільно з М.М. Дрогомижською. У них розглянуто задачу про збіжність лівого та правого рангів матриці над асоціативним кільцем, що має дільники нуля в радикалі Джекобсона, та встановлено критерії ермітовості такого кільця в термінах непервинних головних ідеалів.
Важливі результати П.С. Казімірський отримав для матриць над кільцями диференціальних операторів з коефіцієнтами з однорідного диференціального поля характеристики нуль. Опираючись на встановлене Я.Б. Лопатинським твердження про те, що всі праві ідеали в таких кільцях є не більш ніж двопородженими, він обґрунтував можливість зведення довільної прямокутної матриці з елементами цього кільця до спеціальної форми, у якій перший діагональний блок є одиничною матрицею, а другий – довільною матрицею другого порядку. Цей результат має суттєве значення для теорії систем лінійних диференціальних рівнянь, оскільки показує, що такі системи можна звести до систем, що містять не більш як два рівняння з не більш ніж двома невідомими функціями, застосовуючи лінійні заміни змінних, елементарні перетворення рівнянь і скінченну кількість операцій диференціювання. При цьому процес зведення є фінітарним. П.С. Казімірський також дав абстрактну характеристику кілець диференціальних операторів, установивши умову, яка є дуже близькою до визначальної умови для відомих тепер кілець стабільного рангу 1,5.
П.С. Казімірський спільно зі своїм учнем Б.В. Забавським при дослідженні задачі зведення пари матриць над адекватним кільцем до спеціального трикутного вигляду за допомогою односторонніх ідентичних перетворень встановили нормальну форму матриць щодо таких перетворень.
Однак основна увага П.С. Казімірського була зосереджена на розробці теорії розкладності многочленних матриць i методів розв’язування матричних рівнянь. Відомі на той час методи розв’язування таких задач ґрунтувалися на використанні класичних понять власних і приєднаних векторів, жорданових ланцюгів та інших споріднених конструкцій. П.С. Казімірський, розвинувши одну з ідей свого вчителя Я.Б. Лопатинського, запропонував принципово новий підхід до задач факторизації матричних многочленів. Він базувався на введеному ним у 1964 р. понятті — значенні многочленної матриці на системі коренів відповідного многочлена. Перші роботи П.С. Казімірського в цьому напрямку присвячені розробці методів зображення матричного многочлена A(x), коефіцієнтами якого є матриці n-го порядку над алгебраїчно замкненим полем xapaктеристики нуль, у вигляді добутку A(x)=B(x)C(x), де B(x) – регулярний матричний многочлен із наперед заданим характеристичним многочленом. У цьому напрямі, зокрема, було вказано достатні умови існування лінійних регулярних дільників B(x) (без обмеження загальності надалі ïx можна вважати унітальними, тобто матричними поліномами, старшими коефіцієнтами яких є одинична матриця) матричного многочлена A(x), а також встановлено, що ці умови є необхідними та достатніми, якщо характеристичні многочлени B(x) i C(x) є взаємно простими aбo якщо ïx найбільший спільний дільник є взаємно простим з найбільшим спільним дільником мінорів (n-1)-го порядку матриці A(x). У подальших роботах ці умови поширюються на дільники матричних многочленів довільного степеня. За аналогічних умов запропоновано метод побудови унітальних дільників матричних многочленів i доведено, що в цьому випадку унітальні дільники із заданими характеристичними многочленами визначаються однозначно. Таким чином, була розв’язана задача виділення унітальних множників із матричного многочлена у випадку, коли ці множники однозначно визначаються своїми характеристичними многочленами. Згодом ці результати застосовано до розв’язування відповідних матричних многочленних рівнянь. Зокрема, вказано матричні рівняння, які мають скінченне число розв’язків. У випадку неоднозначності унітальних дільників матричного многочлена із заданими характеристичними многочленами задача їх опису залишалась не розв’язаною.
У 1976 році П.С. Казімірський i В.М. Петричкович ввели поняття напівскалярної еквівалентності многочленних матриць. Цей результат дозволив звести задачу описання дільників матричного многочлена до задачі описання його дільників із наперед заданою формою Сміта. Сумісно з В.Р. Зеліском П.С. Казімірський розв'язав цю задачу спершу в часткових випадках, зокрема при певних обмеженнях на форми Сміта множників. У цілому цю проблему було розв’язано П.С. Казімірського у 1978 році. Одним з ключових понять, на яких ґрунтувався цей результат, було введене ним поняття визначальної матриці, що виступала генератором шуканих унітальних дільників матриці. Одночасно було вказано конструктивний алгоритм побудови таких дільників. Наслідком отриманих результатів стала розробка загального методу розв’язування односторонніх матричних многочленних рівнянь.
Поряд із задачею описання дільників матричних многочленів важливим є питання їх факторизації — тобто подання у вигляді добутку довільного числа множників, зокрема й лінійних, а також визначення класів матричних многочленів, для яких така факторизація завжди можлива. П.С. Казімірський установив необхідні та достатні умови розкладності матричного многочлена на лінійні множники, характеристичні многочлени яких є попарно взаємно простими, а також за умови, що їхній найбільший спільний дільник задовольняє певним очевидним вимогам. Ним було доведено, що унітальний матричний многочлен простої структури (тобто такий, у якого всі елементарні дільники є лінійними) розкладається в добуток лінійних унітальних множників. (Незалежно цей результат також отримали А.С. Маркус, І.В. Мереуца та Л.А. Сахнович). П.С. Казімірський разом із В.М. Петричковичем встановили, що унітальний матричний многочлен, характеристичні корені якого мають кратності не більше двох, є розкладним на лінійні унітальні множники. Насправді наведене ними доведення дає дещо ширший результат: якщо один із коренів характеристичного многочлена унітального матричного многочлена має кратність не більше трьох, а решта – не більше двох, тоді такий матричний многочлен також розкладається в добуток лінійних унітальних множників. Розмірковуючи над цим результатом, П.С. Казімірський висунув гіпотезу про те, що унітальні матричні многочлени, елементарні дільники яких мають степені не більше двох, також розкладаються в добуток лінійних множників. Згодом П.С. Казімірський i В.М. Петричкович довели її правильність для матричного квадратного многочлена. Для матричних многочленів довільних степенів цю гіпотезу підтвердив І.Н. Крупник, доведення якого суттєвим чином базувалось на попередньому результаті. З цих результатів випливає, що коли один з елементарних дільників унітального матричного многочлена має степінь не більше трьох, а решта — не більше двох, то матричний многочлен розкладається в добуток лінійних унітальних множників.
Ще один напрям, якому П.С. Казімірський приділяв значну увагу це задачі про подібність матричних многочленів i скінченних наборів числових матриць. У спільних працях з Л.М. Гринів вони встановили умови звідності матричного многочлена перетворенням подібності до клітково-трикутного та клітково-діагонального виглядів при деяких обмеженнях на характеристичні многочлени діагональних кліток. Згодом задача звідності перетвореннями подібності матричних многочленів над алгебраїчно замкненим полем характеристики нуль до клітково-трикутного вигляду була розв’язана в найбільш загальній ситуації.
У 1981 році було реалізовано давній задум П.С. Казімірського — видання монографії, присвяченої теорії матричних многочленів. До неї увійшли переважно результати, що стосувалися розв’язання проблеми виділення регулярного множника з матричного многочлена та його факторизації. У книзі значну увагу приділено питанням практичного застосування отриманих теоретичних результатів до теорії матричних многочленних рівнянь. Монографія стала основою його докторської дисертації «Розклад матричних многочленів на множники», яку було захищено в Ленінградському університеті в 1985 році. Опонентами були Л.А. Бокуть, Ю.А. Дрозд та А.В. Яковлєв.
У останніх своїх працях П.С. Казімірський разом зі своїми учнями, ґрунтуючись на поняттях напівскалярної еквівалентності многочленних матриць та їх значень на множинах коренів характеристичних многочленів, указав критерії подібності матричних многочленів, характеристичні корені яких є простими, або ж елементарні дільники — попарно взаємно простими. Передчасна смерть перервала його дослідження цієї складної й досі нерозв’язаної проблеми.
Учні П.С. Казімірського, які захистили кандидатські дисертації
-
Уханська Дарія Василівна, Некоторые вопросы разложения полиномиальной матрицы на множители, Кишинівський державний університет, Кишинів, 1968.
-
Луник Фома Павлович, Некоторые вопросы теории элементарных делителей, Кишинівський державний університет імені В.І. Леніна, Кишинів, 1970.
-
Урбанович Марія Миколаївна, К разложению на множители матричного многочлена
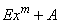 , Інститут математики АН БРСР, Мінськ, 1971.
, Інститут математики АН БРСР, Мінськ, 1971. -
Худий Михайло Іванович, К разложению полиномиальной матрицы на множители, 1971.
-
Дрогомижська Мирослава Миколаївна, Некоторые вопросы теории колец конечно-порождённых правых главных идеалов, Кишинівський державний університет, Кишинів, 1973.
-
Петричкович Василь Михайлович, Вопросы разложимости матричных многочленов на множители и некоторые их связи, Інститут математики АН УРСР, 1977.
-
Зеліско Володимир Романович, Некоторые вопросы факторизации матричных многочленов, Київський державний університет ім. Т.Г. Шевченка, 1980.
-
Шаваровський Богдан Зеновійович, Преобразования подобия матричных многочленов и их разложимость на множители, Інститут математики з ОЦ Академії наук Молдавської РСР, Кишинів, 1986.
-
Забавський Богдан Володимирович, О кольцах элементарных делителей, Інститут математики з ОЦ Академії наук Молдавської РСР, Кишинів, 1987.
-
Щедрик Володимир Пантелеймонович, К вопросу разложимости матричных многочленов на множители, Ленінградський державний університет, 1988.
-
Гринів Любов Михайлівна, Выделение специальных множителей из матричных многочленов, Інститут математики з ОЦ Академії наук Молдавської РСР, Кишинів, 1989.
-
Мельник Орест Михайлович, Некоторые вопросы подобия и факторизации матричных многочленов, Інститут математики з ОЦ Академії наук Молдавської РСР, Кишинів, 1989.
-
Білонога Дарія Михайлівна, Исследование полускалярной эквивалентности некоторых классов многочленных матриц, Інститут математики з ОЦ Академії наук Молдавської РСР, Кишинів, 1992.
Учні П.С. Казімірського, які захистили докторські дисертації
-
Забавський Богдан Володимирович, Діагональна редукція матриць над кільцями, Київський національний університет імені Тараса Шевченка, 2005.
-
Петричкович Василь Михайлович, Узагальнена еквівалентність матриць і їх наборів та факторизація матриць над кільцями, Київський національний університет імені Тараса Шевченка, 2006.
-
Щедрик Володимир Пантелеймонович, Факторизація та одностороння еквівалентність матриць над комутативними областями елементарних дільників, Інститут математики НАН України, 2012.
-
Шаваровський Богдан Зеновійович, Редукція та декомпозиція матриць над поліноміальними кільцями, Інститут математики НАН України, 2013.
Список публікацій П.С. Казімірського
Монографії:
- Казімірський П.С.
Розклад матричних многочленів на множники (видання друге виправлене). – Львів:
Інститут прикладних проблем механіки і математики ім. Я.С.Підстригача НАН України,
2015. – 282 с. pdf.
- Казімірський П.С. Розклад матричних многочленів на множники. – К.: Наукова думка. – 1981. – 224 с.
Статті, автореферати та тези конференцій:
-
Казимирский П.С. Условия совместности неоднородной системы линейных уравнений в некоммутативном кольце главных идеалов // Науч. зап. Львов. политехн. ин-та. Сер. физ.-мат. – 1955. – 30, вып. 1. – С. 45–51.
-
Казимирский П.С. Разложение матрицы с элементами из тела на простые // Науч. зап. Львов. политехн. ин-та. Сер. физ.-мат. – 1956. – Вып. 38, № 2. – С. 110–111.
-
Казимирский П.С. Некоторые общие вопросы линейной алгебры: Автореф. дис. … канд. физ.-мат. наук. – Львов, 1957. – 10 с.
-
Казимирский П.С. Разложение матрицы с элементами из кольца главных идеалов на простые // Докл. Львов. политехн. ин-та. – 1960. – 4, вып. 1, 2. – С. 3–6.
-
Казимирский П.С. Разложение полиномиальной матрицы в произведение матриц первой степени // Докл. Львов. политехн. ин-та. – 1960. – 4, вып. 1, 2. – С. 11–15.
-
Казімірський П.С. Теорема про елементарні дільники для кільця диференціальних операторів // Доп. АН УРСР. – 1962. – № 10. – С. 1275–1278.
-
Казимирский П.С. Теорема об элементарных делителях для кольца дифференциальных операторов // Укр. мат. журн. – 1964. – 16, № 3. – С. 309–318.
-
Казімірський П.С. До розкладу поліноміальної матриці на лінійні множники // Доп. АН УРСР. – 1964. – № 4. – С. 446–448.
-
Казімірський П.С. Про розклад поліноміальної матриці на множники // Доп. АН УРСР. – 1965. – № 7. – С. 847–849.
-
Казімірський П.С., Луник Ф.П. Доповнення однорядкової матриці до оборотної над некомутативним кільцем // Доп. АН УРСР. – 1965. – № 6. – С. 706–710.
-
Казімірський П.С., Луник Ф.П. Доповнення прямокутної оберненої матриці до оборотної // Вестн. Львов. политехн. ин-та. – 1965. – № 8. – С. 61–66.
-
Казімірський П.С. Про розклад поліноміальної матриці на лінійні множники // Вестн. Львов. политехн. ин-та. – 1965. – № 8. – С. 53–60.
-
Казимирский П.С. К разложению квадратной полиномиальной матрицы в произведение линейных множителей // Укр. мат. журн. – 1965. – 17, № 5. – С. 115–119.
-
Казімірський П.С. Про одну необхідну умову розкладності поліноміальної матриці в добуток лінійних множників // Вісн. Львів. політехн. ін-ту. – 1967. – № 16. – С. 93–95.
-
Казімірський П.С. Одне зауваження до теорії областей головних ідеалів // Вісн. Львів. політехн. ін-ту. – 1967. – № 16. – С. 96–97.
-
Казімірський П.С., Уханська Д.В. Розклад поліноміальної матриці на множники // Вісн. Львів. політехн. ін-ту. – 1967. – № 18. – С. 39–45.
-
Берман С.Д., Вольперт А.И., Загорский Т.Я., Казимирский П.С., Костенко В.Г., Лянце В.Э. Ярослав Борисович Лопатинский // Успехи мат. наук. – 1967. – 22. – С. 197–202.
-
Казімірський П.С., Уханська Д.В. Деякі достатні умови розкладу поліноміальної матриці на лінійні множники // Вісн. Львів. політехн. ін-ту. – 1969. – № 31. – С. 51–54.
-
Казімірський П.С. Нормальна форма матриці над кільцем // Вісн. Львів. політехн. ін-ту. – 1970. – № 44. – С. 3–13.
-
Казімірський П.С., Луник Ф.П. Про деякі зв’язки між кільцями типу Прюфера й Ерміта // Вісн. Львів. політехн. ін-ту. – 1970. – № 44. – С. 14–23.
-
Казімірський П.С., Урбанович М.М. Одна достатня умова для розв’язку матричного квадратного рівняння над полем коефіцієнтів // Вісн. Львів. політехн. ін-ту. Сер. фіз.-мат. – 1970. – № 44. – С. 38–43.
-
Казімірський П.С., Луник Ф.П. Дослідження з теорії елементарних дільників // Доп. АН УРСР. Сер. А. – 1970. – № 1. – С. 7–9.
-
Казімірський П.С., Худий М.І. Про один метод виділення лінійного множника з матричного многочлена // Доп. АН УРСР. Сер. А. – 1970. – № 5. – С. 394–396.
-
Казімірський П.С., Дрогомижська М.М. Деякі властивості кілець, дільники нуля яких лежать в радикалі Перліс – Джекобсона // Доп. АН УРСР. Сер. А. – 1971. – № 9. – С. 778–780.
-
Уханська Д.В., Казімірський П.С. Критерій існування кореня -го степеня для довільної матриці // Доп. АН УРСР. Сер. А. – 1971. – № 8. – С. 711–712.
-
Казимирский П.С. Исследования по теории элементарных делителей // Резюме сообщ. и докл. ХІ Всесоюз. алгебр. коллоквиума. – Кишинев, 1971. – С. 73.
-
Казимирский П.С. О разложении матричного многочлена на множители // Резюме сообщ. и докл. ХІ Всесоюз. алгебр. коллоквиума. – Кишинев, 1971. – С. 74.
-
Казімірський П.С. Про виділення регулярного множника з матричного многочлена // Доп. АН УРСР. Сер. А. – 1971. – № 8. – С. 686–687.
-
Казімірський П.С., Луник Ф.П. Доповнення прямокутної оберненої над асоціативним кільцем матриці до оборотної // Доп. АН УРСР. Сер. А. – 1972. – № 6. – С. 505–506.
-
Казімірський П.С., Урбанович М.М. До розкладання матричного двочлена на множники // Доп. АН УРСР. Сер. А. – 1972. – № 5. – С. 209–210.
-
Казімірський П.С. Про розклад матричного многочлена на множники // Укр. мат. журн. – 1972. – 24, № 3. – С. 315–325.
-
Казімірський П.С., Гринів Л.М. Зведення регулярного матричного многочлена до квазітрикутного вигляду // Доп. АН УРСР. Сер. А. – 1972. – № 11. – С. 973–975.
-
Казімірський П.С., Дрогомижська М. М. Зауваження до теорії кілець скінченнопороджених правих головних ідеалів // Укр. мат. журн. – 1973. – 25, № 5. – С. 667–673.
-
Казімірський П.С., Урбанович М. М. Про розклад матричного двочлена на множники // Укр. мат. журн. – 1973. – 25, № 4. – С. 451–461.
-
Казімірський П.С., Петричкович В. М., Шуляр М. А. Канонічна форма для пари комутуючих матриць // Доп. АН УРСР. Сер. А. – 1973. – № 6. – С. 492–495.
-
Казимирский П.С., Грынив Л. М. Выделение «большого» множителя из матричного многочлена // ХІІ Всесоюз. алгебр. коллоквиум: Тез. сообщ. – Свердловск, 1973. – Т. 1. – С. 151.
-
Казимирский П.С., Петричкович В. М. К разложению матричного квадратного трехчлена на линейные множители // ХІІ Всесоюз. алгебр. коллоквиум: Тез. сообщ. – Свердловск, 1973. – Т. 1. – С. 152.
-
Казімірський П.С., Худий М. І. Зображення матричного многочлена в блочному вигляді // Вісн. Львів. політехн. ін-ту. – 1973. – № 75. – С. 14–19.
-
Казимирский П.С., Петричкович В. М. Одно достаточное условие разложимости матричного квадратного трехчлена на линейные множители // II Всесоюз. симп. по теории колец, алгебр и модулей: Резюме сообщ., Кишинев, 21–25 авг. 1974 г. – Кишинев: Штиинца, 1974. – С. 29–30.
-
Казімірський П.С., Гринів Л. М. Виділення «великого» множника із матричного многочлена // Доп. АН УРСР. Сер. А. – 1974. – № 4. – С. 293–297.
-
Казімірський П.С., Гринів Л.М. Зведення регулярного матричного многочлена до квазідіагонального вигляду // Укр. мат. журн. – 1974. – 26, № 3. – С. 316–325.
-
Казимирский П.С. Матричные многочлены и уравнения // Мат. методы и физ.-мех. поля. – 1975. – Вып. 2. – С. 23–31.
-
Казімірський П.С., Петричкович В.М. Зведення матричного квадратного тричлена з комутуючими коефіцієнтами до квазідіагонального виду і його розкладність на лінійні множники // Вісн. Львів. політехн. ін-ту. – 1975. – № 106. – С. 97–102.
-
Казимирский П.С. Выделение из матричного многочлена регулярного линейного множителя простой структуры // Теорет. и прикл. вопросы алгебры и дифференц. уравнений. – Киев: Ин-т математики АН УССР, 1976. – С. 29–40.
-
Грига Б.С., Казимирский П.С. К вопросу единственности выделения унитального множителя из матричного многочлена // Теорет. и прикл. вопросы алгебры и дифференц. уравнений. – Киев: Ин-т математики АН УССР, 1976. – С. 15–18.
-
Казимирский П.С., Зелиско В.Р., Петричкович В.М. О подобии матричных квадратных трехчленов // Теорет. и прикл. вопросы алгебры и дифференц. уравнений. – Киев: Ин-т математики АН УССР, 1976. – С. 40–45.
-
Грига Б.С., Казімірський П.С. До питання єдиності виділення унітального множника з матричного многочлена // Доп. АН УРСР. Сер. А. – 1976. – № 4. – С. 293–295.
-
Казімірський П.С., Зеліско В.Р., Петричкович В. М. До питання про подібність матричних многочленів // Доп. АН УРСР. Сер. А. – 1976. – № 10. – С. 876–878.
-
Казімірський П.С., Зеліско В.Р. Про виділення лінійного множника з матричного многочлена // Доп. АН УРСР. Сер. А. – 1976. – № 11. – С. 968–970.
-
Казимирский П.С. Разложение регулярного матричного многочлена на множители // ІІІ Всесоюз. симп. по теории колец, алгебр и модулей, Тарту, 21–24 сент. 1976 г.: Тез. докл. – Тарту: Тарт. ун-т, 1976. – С. 46.
-
Казимирский П.С., Петричкович В.М. К выделению из полиномиальной матрицы линейного множителя с заданной системой инвариантных многочленов // ІІІ Всесоюз. симп. по теории колец, алгебр и модулей, Тарту, 21–24 сент. 1976 г.: Тез. докл. – Тарту: Тарт. ун-т, 1976. – С. 49.
-
Грига Б.С., Казимирский П.С. Теорема единственности выделения унитального матричного многочлена из полиномиальной матрицы // ІІІ Всесоюз. симп. по теории колец, алгебр и модулей, Тарту, 21–24 сент. 1976 г.: Тез. докл. – Тарту: Тарт. ун-т, 1976. – С. 47.
-
Казимирский П.С., Зелиско В.Р. Однозначность разложения унитального матричного многочлена на множители // ІІІ Всесоюз. симп. по теории колец, алгебр и модулей, Тарту, 21–24 сент. 1976 г.: Тез. докл. – Тарту: Тарт. ун-т, 1976. – С. 48.
-
Казімірський П.С. Розклад регулярного матричного многочлена на множники // Доп. АН УРСР. Сер. А. – 1977. – № 6. – С. 488–490.
-
Казімірський П.С. Необхідність умов розкладу матричного многочлена на лінійні множники // Укр. мат. журн. – 1977. – 29, № 5. – С. 653–658.
-
Казімірський П.С. Квазіунітальні та супровідні матриці матричних многочленів // Теорет. та прикл. питання алгебри і диференц. рівнянь. – К.: Наук. думка, 1977. – С. 29–52.
-
Казімірський П.С., Зеліско В. Р. Про виділення з поліноміальної матриці регулярного множника з наперед заданою формою Сміта // Теорет. та прикл. питання алгебри і диференц. рівнянь. – К.: Наук. думка, 1977. – С. 52–61.
-
Казімірський П.С., Петричкович В.М. Про еквівалентність поліноміальних матриць // Теорет. та прикл. питання алгебри і диференц. рівнянь. – К.: Наук. думка, 1977. – С. 61–66.
-
Зелиско В.Р., Казимирский П.С. К вопросу о разложении матричного многочлена на множители // ХIV Всесоюз. алгебр. конф., Новосибирск, 6–9 сент. 1977 г.: Тез. докл. – Новосибирск, 1977. – Ч. 2. – С. 30–31.
-
Казімірський П.С. Розв’язання проблеми виділення регулярного множника з матричного многочлена // Доп. АН УРСР. Сер. А. – 1978. – № 12. – С. 1075–1078.
-
Казимирский П.С., Луник Ф. П. Дополнение прямоугольной обратной над ассоциативным кольцом матрицы до обратимой // Укр. мат. журн. – 1978. – 30, № 3. – С. 367–370.
-
Казимирский П.С., Петричкович В. М. Разложимость полиномиальной матрицы на линейные множители // Мат. методы и физ.-мех. поля. – 1978. – Вып. 8. – С. 3–9.
-
Казимирский П.С., Зелиско В. Р. К выделению линейного множителя из матричного многочлена // Мат. методы и физ.-мех. поля. – 1978. – Вып. 8. – С. 10–16.
-
Казимирский П.С., Зелиско В. Р. К выделению из полиномиальной матрицы регулярного множителя с заданной формой Смита // Теорет. и прикл. вопросы дифференц. уравнений и алгебра. – Киев: Наук. думка, 1978. – С. 92–96.
-
Казимирский П.С., Шаваровский Б. З. О полускалярной эквивалентности некоторых полиномиальных матриц // Теорет. и прикл. вопросы дифференц. уравнений и алгебра. – Киев: Наук. думка, 1978. – С. 96–100.
-
Казимирский П.С. Решение проблемы выделения регулярного множителя из матричного многочлена // ХV Всесоюз. алгебр. конф., Красноярск, 3–6 июля 1979 г.: Тез. докл. – Красноярск, 1979. – Ч. 2. – С. 69.
-
Казимирский П.С. Решение проблемы выделения регулярного множителя из матричного многочлена // Укр. мат. журн. – 1980. – 32, № 4. – С. 483–498.
-
Казимирский П.С., Грынив Л. М. Приведение конечного набора числовых матриц преобразованием подобия к клеточно-треугольному виду // ІV Всесоюз. симп. по теории колец, алгебр и модулей: Тез. сообщ. – Кишинев, 1980. – С. 31–32.
-
Забавский Б. В., Казимирский П.С. Приведение пары матриц над областью главных идеалов к треугольному виду с формой Смита по главной диагонали применением идентичных левосторонних преобразований // ХVI Всесоюз. алгебр. конф., Ленинград, 22–25 сент. 1981 г.: Тез. докл. – Ленинград, 1981. – Ч. 2. – С. 196.
-
Казимирский П.С., Шаваровский Б. З. К подобию матричных многочленов // ХVI Всесоюз. алгебр. конф., Ленинград, 22–25 сент. 1981 г.: Тез. докл. – Ленинград, 1981. – Ч. 1. – С. 63–64.
-
Казімірський П.С., Шаваровський Б. З. Умови напівскалярної еквівалентності поліноміальних матриць з попарно взаємно простими елементарними дільниками // Доп. АН УРСР. Сер. А. – 1982. – № 8. – С. 11–12.
-
Казимирский П.С., Мельник О.М. К подобию унитальных матричных многочленов // V Всесоюз. симп. по теории колец, алгебр и модулей, Новосибирск, 21–23 сент. 1982 г.: Тез. сообщ. – Новосибирск, 1982. – С. 63–64.
-
Казимирский П.С. Теорема об элементарных делителях в коммутативной области Безу // ХVІI Всесоюз. алгебр. конф., Минск, 14–17 сент. 1983 г.: Тез. сообщ. – Минск, 1983. – С. 94.
-
Забавский Б.В., Казимирский П.С. Приведение пары матриц над адекватным кольцом к специальному треугольному виду применением идентичных односторонних преобразований // Укр. мат. журн. – 1984. – 36, № 2. – С. 256–258.
-
Казимирский П.С. Разложение матричных многочленов на множители: Автореф. дис. … д-ра физ.-мат. наук. – Ленинград, 1984. – 32 с.
-
Казимирский П.С. Теорема единственности решения матричного многочленного уравнения // ХVІІI Всесоюз. алгебр. конф., Кишинев, 11–13 сент. 1985 г.: Тез. сообщ. – Кишинев, 1985. – Ч. 1. – С. 224.
-
Казимирский П.С., Щедрик В.П. Формула общего решения многочленного матричного уравнения // ХVІІI Всесоюз. алгебр. конф., Кишинев, 11–13 сент. 1985 г.: Тез. сообщ. – Кишинев, 1985. – Ч. 1. – С. 225.
-
Казимирский П.С. Решение матричных односторонних многочленных уравнений // ХІХ Всесоюз. алгебр. конф., Львов, 9–11 сент. 1987 г. : Тез. сообщ. – Львов, 1987. – Ч. 1. – С. 122.
-
Казимирский П.С., Мельник О.М. Решение вопроса полускалярной эквивалентности многочленных матриц с попарно различными характеристическими корнями // Докл. АН УССР. Сер. А. – 1988. – № 11. – С. 9–12.
-
Казимирский П.С., Кострикин А.И., Подстригач Я.С. Всесоюзная алгебраическая конференция во Львове // Успехи мат. наук. – 1988. – 43, № 3. – С. 247–249.
-
Казимирский П.С., Мельник О.М. Подобие и строение унитальных матричных квадратных трехчленов с попарно различными характеристическими корнями // Зап. науч. семин. Ленингр. отд-ния Мат. ин-та им. В. А. Стеклова: Кольца и модули. – 1989. – 175. – С. 63–68.
-
Казимирский П.С., Щедрик В.П. О решениях матричных многочленных односторонних уравнений // Докл. АН СССР. – 1989. – 304, № 2. – С. 271–274.
-
Гринив Л.М., Казимирский П.С. Приводимость конечного набора числовых матриц преобразованием подобия к блочно-треугольному виду // Междунар. конф. по алгебре, Новосибирск, 21–26 авг. 1989 г.: Тез. сообщ. по теории колец, алгебр и модулей – Новосибирск, 1989. – С. 42.
-
Казимирский П.С., Калыняк Б.М. О подобии унитальных матричных многочленов простой структуры // Междунар. конф. по алгебре, Новосибирск, 21–26 авг. 1989 г.: Тез. сообщ. по теории колец, алгебр и модулей. – Новосибирск, 1989. – С. 59.
-
Казимирский П.С., Билонога Д.М. Полускалярная эквивалентность многочленных матриц с взаимно простыми элементарными делителями // Докл. АН УССР. Сер. А. – 1990. – № 4. – С. 8–9.